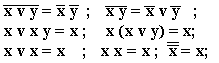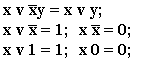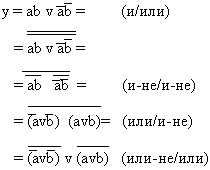Булевы Функции

Основные понятия

Функция f, зависящая от n переменных x₁, x₂, ...., x_n, называется булевой, или переключательной, если функция f и любой из ее аргументов X_i, (i E 1..n) принимают значения только из множества {О, 1}. Аргументы булевой функции также называются булевыми.

Произвольная булева функция задается одним из трех способов: матричным (табличным), геометрическим и аналитическим.При матричном способе булева функция f (х₁, ...,х_n) задается таблицей истинности (табл. 1.1 и 1.2), в левой части которой представлены все возможные двоичные наборы длины n, а в правой указывается значение функции на этих наборах.

Таблица 1.1		Таблица 1.2
х₁х₂х₃		Номер набора
000 001 010 011 100 101 110 111	0 1 0 0 1 1 0 1	0 1 2 3 4 5 6 7	0 1 0 0 1 1 0 1

Под двоичным набором y = < y₁, y₂,...,y_n> yi E {0, 1} понимается совокупность значений аргументов х₁, х₂, ..., x_n булевой функции f. Двоичный набор имеет длину n, если он представлен n цифрами из множества {0,1}. В табл. 1.1 передставлены все двоичные наборы длины 3.
Иногда двоичные наборы в таблице истинности булевой функции удобно представлять номерами наборов. Запишем аргументы х₁, х₂, ..., x_n в порядке возрастания их индексов. Тогда любой двоичный набор y = < y₁, y₂,...,y_n> y_i E {0, 1} можно рассматривать как целое двоичное число N:

N=y₁*2^n-1+y₂*2^n-2+...+y_n

называемое номером набора y. Например, двоичные наборы 101 и 111 имеют номера 5 и 7 соответственно. Очевидно, любая булева функция может быть задана таблицей истинности, в которой двоичные наборы заменены своими номерами (табл. 1.2).
Булевы функции, зависящие от большого числа переменных, задавать таблицей истинности неудобно в силу ее громоздкости. Например, таблица истинности булевой функции 8 переменных будет содержать 2⁸ = 256 строк. Поэтому для задания функций многих переменных удобно использовать модификацию таблицы истинности.
Рассмотрим способ построения такой таблицы истинности для функции n переменных. Множество из n переменных функции разбивается на два подмножества: х₁, х₂, ..., х_j-1 и х_j, х_j+1, ..., х_n. Переменными x₁, x₂, ..., x_n отмечают строки таблицы истинности, задавая в каждой строке значение соответствующего двоичного набора длины j-1. Переменными x_j, x_j+i, ..., x_n отмечают ее столбцы, задавая в каждом столбце значения соответствующего двоичного набора длины n-j+1. Значение функции записывается в клетке на пересечении соответствующей строки и столбца (табл. 1.3).

Таблица 1.3
x₁,x₂,...x_j-1	x_j, x_j+1, ...,x_n
x₁,x₂,...x_j-1	00...0	0...1	...	11...1
00...0			...
00...1			...
...	...	...	...	...
11...1

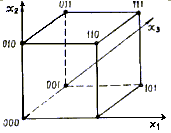
При геометрическом способе булева функция f (х₁, ..., х_n) задается с помощью n-мерного куба. В геометрическом смысле каждый двоичный набор у = <y₁, y₂,...,y_n> y_i E {0,1} есть n-мерный вектор, определяющий точку n-мерпого пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представляется вершинами n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, булева функция, заданная табл. 1.1, геометрически представляется 3-мерным кубом (рис. 1).

При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевых функций занимает особое место в проектировании цифровых автоматов. Фактически, все преобразования над булевыми функциями, необходимые для построения цифровых автоматов, ведутся на аналитическом уровне.
Рассмотрим области определения булевых функций. Как уже отмечалось, между двоичными наборами и двоичными числами существует взаимно однозначное соответствие. Следовательно, существует 2ⁿ различных наборов двоичных переменных.
Таким образом, областью определения булевой функции n переменных при матричном способе задания является множество всех возможных двоичных наборов длины n, а при геометрическом способе задания - множество всех вершин n-мерного единичного куба.
Булеву функцию, определенную на всех своих наборах, называют полностью определенной. В табл. 1.1, 1.2 приведены примеры полностью определенных булевых функций.
Булеву функцию n переменных называют неполностью определенной или частичной, если она определена не на всех двоичных наборах длины n. Неполностью определенная булева функция не попадает под определение, данное в начале , но при произвольном доопределении (на всех наборах, на которых она не определена) это несоответствие снимается.
Легко убедиться, что если булева функция f не определена на m наборах аргументов, то путем ее доопределения можно получить 2^m различных полностью определенных функций. В табл. 1.5 приведен пример неполностью определенной булевой функции трех переменных.

Таблица 1.5
х₁х₂х₃	F
000 001 010 011 100 101 110 111	0 1 - 0 1 - 1 -

Существует не более чем 2^{2^n} различных булевых функций n переменных. К этому выводу легко прийти, пользуясь простыми комбинаторными рассуждениями, и вспомнив, что на каждом из 2ⁿ наборов функции могут принимать два значения.
Функции двух переменных представлены в табл. 1.6.
Наиболее часто употребляются следующие:

Таблица 1.6
х₁х₂	f₀	f₁	f₂	f₃	f₄	f₅	f₆	f₇	f₈	f₉	f₁₀	f₁₁	f₁₂	f₁₃	f₁₄	f₁₅
00 01 10 11	0 0 0 0	0 0 0 1	0 0 1 0	0 0 1 1	0 1 0 0	0 1 0 1	0 1 1 0	0 1 1 1	1 0 0 0	1 0 0 1	1 0 1 0	1 0 1 1	1 1 0 0	1 1 0 1	1 1 1 0	1 1 1 1

f0 (x1, x2) = 0 - тождественный ноль (константа 0);
f1 (x1, x2) = x1 * x2 - конъюнкция. Вместо знака "*" иногда употребляется знак & или /\. Эту функцию часто называют логическим произведением или логическим умножением;
f3 (x1, х2) = x1 - повторение x1;
f5 (x1, x2) = x2 - повторение х2;
f6 (x1, x2) = х1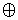

x2 - сложение по модулю 2 или сумма mod 2 (далее +);
f7 (х1, х2) = x1 V x2 - дизъюнкция (логическое ИЛИ);
f8 (x1, x2) = x1 | х2 - функция Вебба (стрелка Пирса);
f9 (х1, х2) = x1 ~ x2 - эквивалентность;
f13(x1, x2) = x1 —> x2 - импликация;
f14(x1, x2) = x1\x2 - штрих Шеффера;
f15(x1, x2) = 1-тождественная единица (константа 1).

Рассмотренные простейшие булевы функции позволяют строить новые булевы функции с помощью обобщенной операции, называемой операцией суперпозиции. Фактически операция суперпозиции заключается в подстановке вместо аргументов других булевых функций (в частности аргументов). Например, из функции f1 (x1, x2) с помощью подстановки f3 (х4, x8), f2 = x3 вместо аргументов х1 и х2 соответственно получаем функцию f1 (f3 (x4, x8), x3). Последняя от переменных х1, и х2 уже не зависит.
Отметим, что реально элементарной функции соответствует реализующий ее элемент, а суперпозиции булевых функций соответ-ствует соединение элементов

Операция суперпозиции позволяет увидеть качественный переход от n = 1 к n = 2. Действительно, суперпозиция функций одного аргумента порождает функции одного аргумента. Суперпозиция функций двух аргументов дает возможность строить функции любого числа аргументов (в приведенном примере построена функция трех переменных).
Суперпозиция булевых функций представляется в виде логических формул. Однако следует отметить:

одна и та же функция может быть представлена разными формулами;
каждой формуле соответствует своя суперпозиция и, следова-тельно, своя схема соединений элементов;
между формулами представления булевых функций и схемами, их реализующими, существует взаимооднозначное соответствие.

Очевидно, среди схем, реализующих данную функцию, есть наи-более простая. Поиск логической формулы, соответствующей этой схеме, представляет большой практический интерес, а преобразование формул булевых функций основано на использовании соотноше-ний булевой алгебры.
Для булевой алгебры определены одна одноместная (унарная) операция "отрицание", две двухместные (бинарные) операции конъюнкция и дизъюнкция (обозначаются "*" (прим. далее "*" упускается), "v" соответственно).
В этой алгебре справедливы три аксиомы:

закон коммутативности - х v у = у V х, ху = ух;
закон ассоциативности - (х v у) v z = х v(y v z), (х y) z = х(у z);
закон дистрибутивности - х (у v x) = ху v хz, х v y * z = (х v y)(х v z).

Под бинарной операцией на множестве А, в общем случае пони-мают отображение декартового произведения множеств (A Х А) в множество А. Иными словами, результат применения бинарной операции к любой упорядоченной паре элементов из А есть также элемент из множества А.
Под унарной операцией на множестве А понимают выделение (фиксацию) какого-либо элемента множества А.
Преобразование формул булевых функций применением только аксиом булевой алгебры малоэффективно. Для упрощения формул используется целый ряд соотношений.

Теоремы де Моргана

Алгебра Жегалкина

В ряде случаев, преобразования над формулами булевых функ-ций удобно призводить в алгебре Жегалкина.
Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение по модулю 2 (*,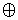

(прим. далее + ) ), а также константу 1. Здесь имеют место те же законы:

х + y = y + х, х у = у х (закон коммутативности);
х + (у + z) = (х + у) + z, х(у z) = (х у)z (закон ассоциативности);
x (y + z) = x y + x z (закон дистрибутивности).

Для упрощения формул могут быть использованы следующие соотношения:
х + 0 = х;
х 1 = х;
х 0 = 0;
х + х = 0;
х х = х.
Из коммутативности и ассоциативности дизъюнкции следует, что дизъюнкция нескольких переменных может выполняться последовательно, причем порядок взятия дизъюнкции не влияет на результат."

Использованная литература:
1) "Прикладная теория цифровых автоматов"    Киев "Вища Школа" 1987
    К.Г. Самофалов, А.М. Романкевич, В.Н. Валуйский,
    Ю.С. Каневский, М.М. Пиневич
    страницы (183 - 189).