<==Back
Булевы Функции
Аналитическое представление булевых функций.
"Выше упомяналось осуществовании аналитических форм представления булефых функций, были приведены простейшие примеры. Здесь рассмотрим
универсальные (канонические) формы представления, дающие возможность
получить аналитическую форму непосредственно по таблице истинности
для произвольной булевой функции. Эта форма в дальнейшем может быть
упрощена. Поскольку между множеством аналитических представлений и
множеством схем, реализующих булеву функцию, существует взаимно-однозначное соответствие, отыскание канонической фоорм представления булевой функции является начальным этапом синтеза схемы,
ее реализующей. Наиболее широкое распостранение получила
совершенная дизъюнктивная нормальная форма (СДНФ). Прежде чем пререйти к её изучению, приведем определение конституенты еденицы - понятия, которым будем широко пользоватся в дальнейшем.
Конституента 1 - функция f(x1, x2, ... xn) принимающая значение 1 только на единственном наборе.
Конституента 1 записывается как логическое произведение n различных
булевых переменных, некоторые из них могут быть с отрицаниями. Например,
х1/х2/х3х4 - элементарное логическое произведение, являющееся конституентой еденицы переменных
х1,х2,х3,х4 принимает значение
1 на единственном наборе 1001. Понятно, что на остальных 15 наборах эта
конституента единицы равна нулю.
Ели вспомнить, что дизъюнкция равна 1, когда хотя бы одна из переменных
принимает значение 1, то можно легко выразить любую булеву функцию как дизъюнкцию конституент единицы, соответствующих тем наборам, на которых
функция равна 1. В более общем виде это можно записать следующим образом:
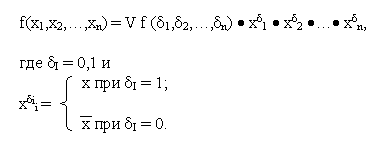
Эта форма и есть СДНФ. Заметим, что наборы, на которых функция f принимает
значение 1, часто называются единичными, остальные - нулевыми наборами.
Выписывать в СДНФ имеет смысл толькр конституенты единицы, соответствующие единичным наборам.
ПРИМЕР :
| Таблица 2.1 |
|
|
|
х1х2х3 |
F1 |
F2 |
| 000 |
0 |
0 |
| 001 |
1 |
0 |
| 010 |
1 |
0 |
| 011 |
0 |
1 |
| 100 |
0 |
0 |
| 101 |
0 |
1 |
| 110 |
0 |
1 |
| 111 |
1 |
1 |
F1=/x1/x2x3 v
/x1x2/x3 v
x1x2x3
F2=/x1x2x3 v
x1/x2x3 v
x1x2/x3 v
x1x2x3
Другая известная форма носит название совершенной конъюнктивной нормальной формы (СКНФ). Она строится аналогично СДНФ.
Конституента 0 - функция f(x1, x2, ... xn) принимающая значение 0 только на единственном наборе.
Конституента нуля записывается в виде элементарной дизъюнкции всех переменных. Каждому набору соответствует своя конституента 0. Например,
набору 0110 переменных х1х2х3х4 соответствует конституента нуля
х1 v /х2 v /х3 v х4.
СКНФ представляется как конъюнкция конституент нуля, соответствующих нулевым наборам функции."
ПРИМЕР. Для рассмотренных функций в табл. 2.1 построим СКНФ:
F1=(x1 v x2 v x3)
(x1 v /x2 v /x3)
(/x1 v x2 v x3)
(/x1 v x2 v /x3)
(/x1 v /x2 v x3)
F2=(x1 v x2 v x3)
(x1 v x2 v /x3)
(x1 v /x2 v x3)
(/x1 v x2 v x3)
Использованная литература:
1) "Прикладная теория цифровых автоматов" Киев "Вища Школа" 1987
К.Г. Самофалов, А.М. Романкевич, В.Н. Валуйский,
Ю.С. Каневский, М.М. Пиневич
страницы (189 - 190).